Unterrichtsmaterialien Mathematik: Gymnasium
795 MaterialienIn über 795 Dokumenten und Arbeitsblättern für das Fach Mathematik: Gymnasium findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Mehr Themen
Auswählen
Auswählen
Auswählen
Auswählen
795 Materialien
Einheit
Ergebnissicherung und DefinitionM5 Der Differenzenquotient als mittlere Änderungsrate; M6/M7 Üben, üben, üben – Tandembögen
Definitionsbereich
10. Klasse
Gymnasium
3 SeitenDefinitionsbereich10. KlasseGymnasium3 SeitenTesten kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
Die Definitionen auf einen BlickDie Schüler wiederholen die Definitionen der verschiedenen Zahlen.
Definitionsbereich8. KlasseGymnasium1 SeiteDefinitionsbereich8. KlasseGymnasium1 Seite
Einheit
Teil I: „Graphen“, „Wege in Graphen“ – einige GrundbegriffeWo geht’s denn hier zu ...?; Was ist ein „Graph“?; Wege in Graphen
Graphen10-13. KlasseGesamtschule3 SeitenGraphen10-13. KlasseGesamtschule3 Seiten
video
Lineare Gleichungen - grafische DarstellungWie kann man lineare Gleichungen grafisch darstellen? Das Verfahren ist ganz einfach: Es wird gezeigt, wie man Wertepaare aus einer Tabelle in das Koordinatensystem überträgt. Die Funktionsvorschrift der linearen Funktion wird erläutert, und anhand von Beispielen werden unterschiedliche Graphen gezeichnet.
Analysis5-13. KlasseGesamtschuleAnalysis5-13. KlasseGesamtschuleVerwandte Themen
Einheit
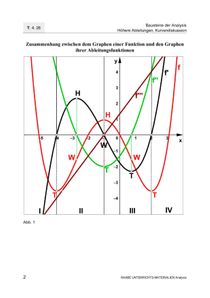
Zusammenhang zwischen dem Graphen einer Funktion und den Graphen ihrer AbleitungsfunktionenZusammenhang zwischen dem Graphen einer Funktion und den Graphen ihrer Ableitungsfunktionen
Graphen11-13. KlasseBerufliche Schule10 SeitenGraphen11-13. KlasseBerufliche Schule10 Seiten
Einheit
Lebendige Graphen - Graphen von Funktionen auf dem Schulhof nachstellenMeine 10. Klasse arbeitet gerade mit Exponentialfunktionen. Beim Unterthema „Prognosen“ tauchen auch lineare Funktionen auf. Was war das nochmal? Eigentlich bin ich genervt, dass solche Grundlagen nicht abrufbar sind. Aber so ist eben der Schulalltag! Meine Antwort: In der nächsten Stunde gehe ich mit der ganzen Klasse auf den Schulhof.
Graphen7-8. KlasseSekundarstufe 12 SeitenGraphen7-8. KlasseSekundarstufe 12 Seiten
Einheit
Untersuchung einer ExponentialfunktionFunktionsuntersuchungen mit Eigenschaftsbestimmungen gehören zu den Standardaufgaben des Analysis-Unterrichts der Oberstufe. Ebenso können Figuren zwischen den Graphen der Funktion und der x-Achse gelegt werden, sodass der Flächeninhalt maximal wird. Die Funktionsuntersuchung erweitert der Beitrag damit um Extremalwertaufgaben. Nimmt man zum Graph einer Funktion noch den Graphen der Ableitungsfunktion hinzu, so kann man nicht nur Flächenberechnungen zwischen dem Graphen der Ausgangsfunktion und der x-Achse, sondern auch zwischen den Graphen von Funktion und Ableitungsfunktion durchführen. Der Graph der Exponentialfunktion bildet bei einer weiteren Aufgabe den Querschnitt eines Körpers, bei dem die Jugendlichen bestimmte Größen berechnen. Ebenso bildet der in Richtung der x-Achse gestreckte Graph den Querschnitt einer Steilküste. Anwendungsaufgaben stellen bestimmte Anforderungen an diese Steilküste, welche die Lernenden lösen.
Graphen11-13. KlasseBerufliche Schule27 SeitenGraphen11-13. KlasseBerufliche Schule27 Seiten
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
