Unterrichtsmaterialien Mathematik: Berufliche Schule
183 MaterialienIn über 183 Dokumenten und Arbeitsblättern für das Fach Mathematik: Berufliche Schule findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Mehr Themen
Auswählen
Auswählen
Auswählen
Auswählen
183 Materialien
Einheit
Anwendung von Matrizen - M6-M8Übungsaufgaben zum Rechnen mit Matrizen; Matrizen bei Produktionsprozessen; Matrizen bei Populationen
Matrizen
11-13. Klasse
Berufliche Schule
10 SeitenMatrizen11-13. KlasseBerufliche Schule10 SeitenTesten kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
Kryptografie - M5-M9Übungsaufgaben; Die Caesar-2-Codierung; Die Spiegelung mithilfe von Matrizen; Übungsaufgaben mit Matrizen; Gestufte Hilfen zu den Aufgaben
Matrizen10-13. KlasseBerufliche Schule8 SeitenMatrizen10-13. KlasseBerufliche Schule8 Seiten
Einheit
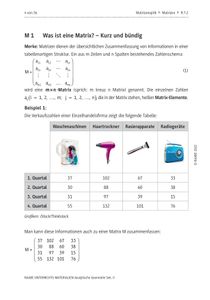
Matrizen – M1-M7M1 Was ist eine Matrix? – Kurz und bündig; M2 Rechnen mit Matrizen – was man wissen sollte; M3 Rechnen mit Matrizen – Übungsaufgaben; M4 Optische Grundlagen – kurz und bündig; M5 Strahlvektor und Transfermatrix; M6 Transfermatrix der geradlinigen Ausbreitung; M7 Transfermatrix der Brechung an ebener Grenzschicht;
Matrizen11-13. KlasseBerufliche Schule10 SeitenMatrizen11-13. KlasseBerufliche Schule10 Seiten
Einheit
Matrizen – M8-M15M8 Transfermatrix der dünnen Linse; M9 Transfermatrix eines optischen Systems; M10 Transfermatrix eines optischen Systems – Übungen; M11 Transfermatrix zweier dünner Linsen ohne Abstand; M12 Transfermatrix des astronomischen Fernrohrs; M13 Transfermatrix der optischen Abbildung durch eine Linse; M14 Zusammenfassung Matrizenoptik – kurz und bündig; M15 Sind Sie fit? – Lernerfolgskontrolle zur Matrizenoptik;
Matrizen11-13. KlasseBerufliche Schule14 SeitenMatrizen11-13. KlasseBerufliche Schule14 SeitenVerwandte Themen
Einheit
Quadratisches gleichseitiges AntiprismaM1 Definition von Antiprismen; M2 Quadratisches gleichseitiges Antiprisma (Höhe); M3 Zusatzaufgaben; M4 Winkelberechnungen; M5 Eingefügte Pyramide und Volumen
Antiproportionalität11-13. KlasseBerufliche Schule6 SeitenAntiproportionalität11-13. KlasseBerufliche Schule6 Seiten
Verhältnisse11-13. KlasseBerufliche Schule2 Seiten
Einheit
Eine runde SacheNur eine Funktion mit einer einzelnen unabhängigen Variablen ist die notwendige Voraussetzung für die Lösung einer solchen Extremwertaufgabe. Da sich aus der Aufgabenstellung meist Funktionsgleichungen mit zwei oder mehreren unabhängigen Variablen ergeben, sind die Nebenbedingungen erforderlich mit deren Hilfe dieses Ziel – Funktionsgleichungen mit genau einer unabhängigen Variablen – erreicht werden kann. Das Ermitteln dieser Nebenbedingungen ist das eigentliche Problem. Dabei helfen in der Regel Skizzen, die den Sachverhalt der Aufgabenstellung prinzipiell darstellen und so das Finden der Lösungsidee erleichtern. Den Schülerinnen und Schülern wird auch bewusst, wie wichtig der Nachweis der rechnerisch ermittelten lokalen Extrema ist, um für das zu lösende Problem falsche bzw. nicht sinnvolle Ergebnisse auszuschließen.
Variablen11-13. KlasseBerufliche Schule26 SeitenVariablen11-13. KlasseBerufliche Schule26 Seiten
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
