Unterrichtsmaterialien Mathematik: Wahrscheinlichkeitstheorie
163 MaterialienIn über 163 Dokumenten und Arbeitsblättern für das Fach Mathematik: Wahrscheinlichkeitstheorie findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Mehr Themen
Auswählen
Auswählen
Auswählen
Auswählen
163 Materialien
Einheit
LösungenWählt man für den Parameter bei einer Punkte-, Geraden- oder Ebenenschar einen gültigen Zahlenwert, so erhält man genau einen Punkt, eine Gerade oder eine Ebene. In mehreren Aufgaben überprüfen die Schülerinnen und Schüler die Lagebeziehung von Punkten der Schar zu einer Geraden bzw. zu einer Ebene oder von Geraden einer Schar zu einer Ebene. Die Lernenden bestimmen den Parameter so, dass bestimmte Eigenschaften wie die Gleichschenkligkeit von Dreiecken erfüllt sind. Die Bestimmung des Parameters kann auch zu einem Extremwertproblem führen, bei dem die Jugendlichen die Extremstellen ermitteln. Dabei zeigt sich, dass sich auch Methoden der Analysis in Aufgaben aus dem Bereich der analytischen Geometrie anwenden lassen.
Ableitung
11-13. Klasse
Berufliche Schule
19 SeitenAbleitung11-13. KlasseBerufliche Schule19 SeitenTesten kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
InformationWählt man für den Parameter bei einer Punkte-, Geraden- oder Ebenenschar einen gültigen Zahlenwert, so erhält man genau einen Punkt, eine Gerade oder eine Ebene. In mehreren Aufgaben überprüfen die Schülerinnen und Schüler die Lagebeziehung von Punkten der Schar zu einer Geraden bzw. zu einer Ebene oder von Geraden einer Schar zu einer Ebene. Die Lernenden bestimmen den Parameter so, dass bestimmte Eigenschaften wie die Gleichschenkligkeit von Dreiecken erfüllt sind. Die Bestimmung des Parameters kann auch zu einem Extremwertproblem führen, bei dem die Jugendlichen die Extremstellen ermitteln. Dabei zeigt sich, dass sich auch Methoden der Analysis in Aufgaben aus dem Bereich der analytischen Geometrie anwenden lassen.
Ableitung11-13. KlasseBerufliche Schule1 SeiteAbleitung11-13. KlasseBerufliche Schule1 Seite
Einheit
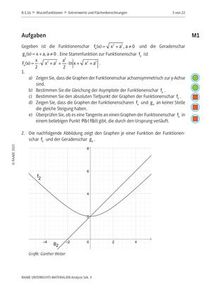
Extremwertprobleme und Flächenberechnungen bei einer WurzelfunktionenscharBei einer Wurzelfunktionenschar und einer Geradenschar, die oft fälschlicherweise von Schülerinnen und Schülern aus der Wurzelfunktionenschar hergeleitet wird, werden die Parameter bestimmt, sodass bestimmte Eigenschaften vorliegen. Erweitert werden diese Aufgabenstellungen noch um Aufgaben zur Flächenberechnung von Dreiecken sowie zur Volumenberechnung von Körpern, die bei der Rotation eines Graphen um die x-Achse entstehen.
Ableitung11-13. KlasseBerufliche Schule21 SeitenAbleitung11-13. KlasseBerufliche Schule21 Seiten
Einheit
LösungenZwei feste Punkte A und B bilden mit einem Punkt einer Punkteschar Ck eine Dreieckschar. Die Schülerinnen und Schüler zeigen, dass alle Punkte der Schar auf einer Geraden liegen und dass alle Dreiecke gleichschenklig sind. Sie bestimmen die Parameter der Punkte Ck, sodass das entstehende Dreieck gleichseitig bzw. rechtwinklig ist, und stellen eine von k abhängige Flächeninhaltsfunktion für die Dreiecke auf. Mit den Methoden der Analysis untersuchen sie diese Funktion bei eingeschränktem Definitionsbereich. Stochastische Überlegungen kommen ins Spiel, wenn die Jugendlichen mittels einer Unterteilung der entstehenden Flächeninhalte in vier Gruppen Ereignisse festlegen, deren Lösung mithilfe von (gekürzten) Baumdiagrammen oder der Binomialverteilung erfolgt.
Analysis11-13. KlasseBerufliche Schule20 SeitenAnalysis11-13. KlasseBerufliche Schule20 Seiten
Einheit
EinführungZwei feste Punkte A und B bilden mit einem Punkt einer Punkteschar Ck eine Dreieckschar. Die Schülerinnen und Schüler zeigen, dass alle Punkte der Schar auf einer Geraden liegen und dass alle Dreiecke gleichschenklig sind. Sie bestimmen die Parameter der Punkte Ck, sodass das entstehende Dreieck gleichseitig bzw. rechtwinklig ist, und stellen eine von k abhängige Flächeninhaltsfunktion für die Dreiecke auf. Mit den Methoden der Analysis untersuchen sie diese Funktion bei eingeschränktem Definitionsbereich. Stochastische Überlegungen kommen ins Spiel, wenn die Jugendlichen mittels einer Unterteilung der entstehenden Flächeninhalte in vier Gruppen Ereignisse festlegen, deren Lösung mithilfe von (gekürzten) Baumdiagrammen oder der Binomialverteilung erfolgt.
Analysis11-13. KlasseBerufliche Schule4 SeitenAnalysis11-13. KlasseBerufliche Schule4 Seiten
Einheit
EinführungDas Angebot an Apps, digitalen Lernplattformen und Lernspielen wächst stetig – aber welche sind für meinen Unterricht wirklich lernförderlich? Wir stellen Ihnen einige digitale Lernmedien zu zentralen Themen für unterschiedliche Klassenstufen an praktischen Beispielen vor. Computer, Smartphones und Apps: Die Vielzahl angebotener digitaler Lernmedien auch für den Matheunterricht bietet eine Fülle an Möglichkeiten, die Inhalte lebendiger und zugänglicher zu vermitteln – man läuft aber auch Gefahr, den Überblick zu verlieren. Hier wollen wir Orientierung bieten. Bewährte und innovative digitale Lernmedien werden anhand fünf zentraler Qualitätsmerkmale für den Mathematikunterricht (kognitive Aktivierung, Verstehensorientierung, Lernendenorientierung und Adaptivität, Kommunikationsförderung, Durchgängigkeit) verortet und ihr Einsatz im Unterricht beschrieben. Aus dem Inhalt: Welches Tool ist passend? – Mathematikspezifische digitale Lernmedien: Kriterien für Auswahl und Einsatz; Was bedeutet eigentlich pro? – Multiplikative Textaufgaben mit Bildern lösen; X-Bert und die ganzen Zahlen – Ein digitales Lernspiel festigt das (Kopf-)Rechnen; Lineare Funktionen mit ASYMPTOTE – Grundvorstellungen digital fördern und diagnostizieren; Konfidenzintervalle verstehensorientiert unterrichten – Das Urnenmodell als Verständnisanker in einer digital angereicherten Lernumgebung; Warum nicht mal diagonal? Vierecke ordnen mit dem Heidelberger Winkelkreuz.
Angewandte Mathematik5-13. KlasseSekundarstufe3 SeitenAngewandte Mathematik5-13. KlasseSekundarstufe3 Seiten
Einheit
InformationDas Angebot an Apps, digitalen Lernplattformen und Lernspielen wächst stetig – aber welche sind für meinen Unterricht wirklich lernförderlich? Wir stellen Ihnen einige digitale Lernmedien zu zentralen Themen für unterschiedliche Klassenstufen an praktischen Beispielen vor. Computer, Smartphones und Apps: Die Vielzahl angebotener digitaler Lernmedien auch für den Matheunterricht bietet eine Fülle an Möglichkeiten, die Inhalte lebendiger und zugänglicher zu vermitteln – man läuft aber auch Gefahr, den Überblick zu verlieren. Hier wollen wir Orientierung bieten. Bewährte und innovative digitale Lernmedien werden anhand fünf zentraler Qualitätsmerkmale für den Mathematikunterricht (kognitive Aktivierung, Verstehensorientierung, Lernendenorientierung und Adaptivität, Kommunikationsförderung, Durchgängigkeit) verortet und ihr Einsatz im Unterricht beschrieben. Aus dem Inhalt: Welches Tool ist passend? – Mathematikspezifische digitale Lernmedien: Kriterien für Auswahl und Einsatz; Was bedeutet eigentlich pro? – Multiplikative Textaufgaben mit Bildern lösen; X-Bert und die ganzen Zahlen – Ein digitales Lernspiel festigt das (Kopf-)Rechnen; Lineare Funktionen mit ASYMPTOTE – Grundvorstellungen digital fördern und diagnostizieren; Konfidenzintervalle verstehensorientiert unterrichten – Das Urnenmodell als Verständnisanker in einer digital angereicherten Lernumgebung; Warum nicht mal diagonal? Vierecke ordnen mit dem Heidelberger Winkelkreuz.
Angewandte Mathematik5-13. KlasseSekundarstufe1 SeiteAngewandte Mathematik5-13. KlasseSekundarstufe1 Seite
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
