Unterrichtsmaterialien Mathematik: Winkel
84 MaterialienIn über 84 Dokumenten und Arbeitsblättern für das Fach Mathematik: Winkel findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Mehr Themen
Auswählen
Auswählen
Auswählen
Auswählen
84 Materialien
Einheit
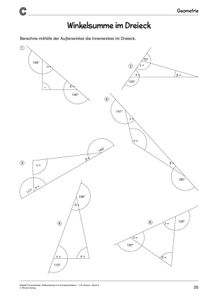
Geometrie – Kompetenzstufe BWinkelsumme im Dreieck; Dreiecke konstruieren I; Dreiecke konstruieren II; Flächeninhalt von Dreiecken; Der Kreis; Kreisfläche und Kreisumfang; Das „Haus der Vierecke“; Winkelsumme im Viereck; Umfang und Flächeninhalt von Parallelogramm und Trapez berechnen; Regelmäßige Vielecke konstruieren; Raummaßeinheiten – Domino; Geometrische Körper – Formeln; Zylindernetze zeichnen; Volumen und Oberfläche von Dreiecksprisma und Zylinder berechnen
Flächen
7. Klasse
Sekundarstufe 1
16 SeitenFlächen7. KlasseSekundarstufe 116 SeitenTesten kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
Geometrie – Kompetenzstufe CWinkelsumme im Dreieck; Dreiecke konstruieren I; Dreiecke konstruieren II; Flächeninhalt von Dreiecken; Der Kreis; Kreisfläche und Kreisumfang; Das „Haus der Vierecke“; Winkelsumme im Viereck; Umfang und Flächeninhalt von Parallelogramm und Trapez berechnen; Regelmäßige Vielecke konstruieren; Raummaßeinheiten – Domino; Geometrische Körper – Formeln; Unvollständige Zylindernetze; Volumen und Oberfläche von Dreiecksprisma und Zylinder berechnen
Flächen7. KlasseSekundarstufe 116 SeitenFlächen7. KlasseSekundarstufe 116 Seiten
Einheit
Geometrie - Teil 1Winkelsumme im Dreieck; Dreiecke konstruieren: Seite – Seite – Seite; Dreiecke konstruieren: Seite – Winkel – Seite; Dreiecke konstruieren: Winkel – Seite – Winkel; Dreiecke konstruieren: Seite – Seite – Winkel; Umfang von Dreiecken berechnen; Flächeninhalt von Dreiecken berechnen; Der Kreis I; Der Kreis II; Kreisfläche berechnen; Kreisumfang berechnen
Flächen7. KlasseSekundarstufe 111 SeitenFlächen7. KlasseSekundarstufe 111 Seiten
video
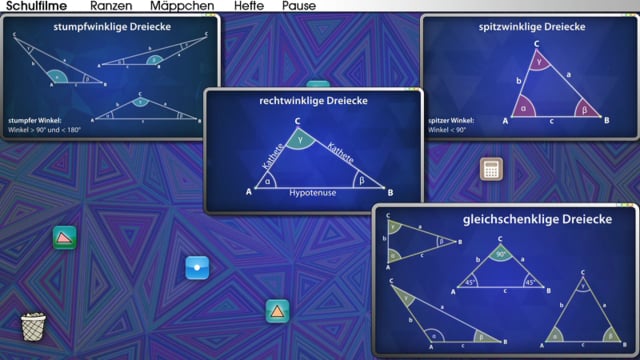
Dreiecke - Arten, Winkel, Umfang, FlächeAlle wichtigen Informationen rund ums Dreieck bietet dieser Kurzfilm. Die Punkte, Seiten, Winkel und Höhen werden benannt. Unterschiedliche Formen des Dreiecks und der Winkel werden vorgestellt. Schließlich wird gezeigt, wie man den Umfang und den Flächeninhalt der geometrischen Figur errechnen kann.
Flächen5-11. KlasseGesamtschuleFlächen5-11. KlasseGesamtschuleVerwandte Themen
Einheit
Vorstellungsorientierter TrigonometrieunterrichtVorstellungsorientierter Trigonometrieunterricht
Berechnung von Winkelgrößen5-13. KlasseSekundarstufe13 SeitenBerechnung von Winkelgrößen5-13. KlasseSekundarstufe13 Seiten
Einheit
GeoGebra - dynamische Geometriesoftware gewinnbringend einsetzen - Teil 1M1 Erste Schritte – Koordinatengitter und Symbolleiste; M2 Figuren und Formen – mit GeoGebra zeichnen; M3 Erstelle deine eigenen Mandalas! – Kreise und Vielecke; M4 Die Winkelsumme im Dreieck – Dreiecke vergleichen; M5 Hierauf musst du achten!; M6 Mit GeoGebra eine Achsenspiegelung durchführen; M7 Eigenschaften der Achsenspiegelung; M8 Lineare Funktionen – was passt zusammen?; M9 Grafische Lösung linearer Gleichungssysteme; M10 Eigenschaften der zentrischen Streckung; M11 Wie konstruiert man eine zentrische Streckung?; M12 Bungeespringen – beschleunigte Bewegungen darstellen
Dynamische Geometriesoftware9-11. KlasseGymnasium12 SeitenDynamische Geometriesoftware9-11. KlasseGymnasium12 Seiten
video
Mittelsenkrechte und WinkelhalbierendeDie Mittelsenkrechte und die Winkelhalbierende lassen sich auch ohne ein Geodreieck bestimmen: Der Film zeigt die Verfahren, die auch schon im antiken Griechenland angewendet worden sind. Dafür reichen ein Lineal und ein Zirkel aus, da man nur die Schnittpunkte korrekt erstellter Kreise dafür finden muss.
Geodreieck5-10. KlasseGymnasiumGeodreieck5-10. KlasseGymnasium
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner
Probezeit, entstehen für dich keine Kosten. 🚀
Probezeit, entstehen für dich keine Kosten. 🚀
