Unterrichtsmaterialien Mathematik: Zahlenfolgen

67 Materialien

In über 67 Dokumenten und Arbeitsblättern für das Fach Mathematik: Zahlenfolgen findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!

Nachbarzahlen

Vorgänger – Nachfolger

Zahlen ordnen

Zahlenreihe

Mehr Themen

Fach

Auswählen

Biologie Chemie Deutsch als Zweitsprache Deutsch Didaktik & Methodik Englisch Erdkunde Französisch Geschichte Kunst LateinMathematikMusik Philosophie Physik Politik Religion Spanisch Sport Wirtschaft

Schultyp

Auswählen

Grundschule Hauptschule Realschule Gesamtschule Gymnasium Förderschule Berufliche Schule Sekundarstufe I Sekundarstufe II

Klassenstufe

Auswählen

1 2 3 4 5 6 7 8 9 10 11 12 13

Verlag

Auswählen

Ärzte Ohne Grenzen Auer Verlag Aulis Bange Verlag Betzold BMVI Carl-Auer Verlag Deutsche Flugsicherung dpa-infografik EDEOS eDidact elk Verlag Ernst Klett Sprachen ESRI Freiwillige Selbstkontrolle Multimedia Friedrich Verlag Herolé Klett Kallmeyer Klett Lerntraining Klett MEX Klinkhardt Klippert Medien Langenscheidt Lernbiene Let's MINT Medienblau MedienLB Mildenberger Verlag Oxfam Persen Verlag Picture-Alliance PONS RAABE SchiLf Akademie Schulfilme im Netz scolix TerraX UNICEF UTB Vandenhoeck & Ruprecht Waxmann Welttierschutzgesellschaft Wheelmap YAEZ

67 Materialien

Flexibler Bereich: Meine Zahlen - Zahlenwörter lesen und schreiben

Einheit

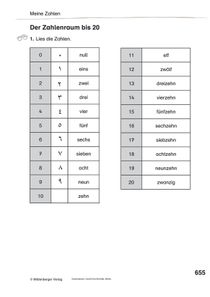
Flexibler Bereich: Meine Zahlen - Zahlenwörter lesen und schreiben

Die Schülerinnen und Schüler lesen Zahlwörter, schreiben sie in ein Gitterrätsel und ordnen Zahlwörter der entsprechenden symbolischen Darstellung zu.

Arithmetik

1-10. Klasse

Gesamtschule

5 Seiten

Arithmetik

1-10. Klasse

Gesamtschule

5 Seiten

Testen kostet nichts

Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀

Jetzt kostenlos testen

Einheit

Rätselspaß Adventskalender - Teil 1

Bewegung in der Fläche; Ablesen im Diagramm; Beschriftung der y-Achse; Flächen aus Figuren; Aufstellen und Berechnen eines Terms; Kleine kombinatorische Überlegungen; Zahlenrätsel; Logische Fortsetzung einer Zahlenreihe; Messen und Maßstab; Textverständnis; Aufstellen und Berechnen eines Terms; Umgang mit dem Zirkel; Logische Fortsetzung einer Figurenreihe; Zerlegen einer Zahl in Vielfache der 5 und der 3; Uhrzeit: analog und digital; Zeichnen eines Weges mithilfe von Himmelsrichtungen; Addition bzw. Subtraktion von Brüchen

Angewandte Mathematik

5. Klasse

Gesamtschule

8 Seiten

Angewandte Mathematik

5. Klasse

Gesamtschule

8 Seiten

Allgemeine Entwicklung der Zahlenverarbeitung und der Rechenleistungen

Einheit

Allgemeine Entwicklung der Zahlenverarbeitung und der Rechenleistungen

Zahlenverständnis bei Tieren; Präverbales Verständnis von Numerositäten bei Babys; Theoretische Modelle der präverbalen Verarbeitung von Numerositäten; Die Entwicklung des Zählens; Symbolische Repräsentation von Numerositäten: Zahlwörter, arabische Zahlen und Transkodieren; Erwerb der arithmetischen Kompetenzen; Fingerrechnen; Der Übergang vom zählenden Rechnen zum Abruf von arithmetischen Fakten; Auswahl der besten Rechenstrategie; Intuitive und kulturelle Mathematik; Geschlechtsunterschiede; Leistungsmotivation, Selbstbild, Emotion und Rechenleistung; Modelle der Entwicklung der Rechenleistung

Angewandte Mathematik

1-13. Klasse

Grundschule

47 Seiten

Angewandte Mathematik

1-13. Klasse

Grundschule

47 Seiten

Einheit

Einführung

Was sind rationale Zahlen?; Allgemeines zu rationalen Zahlen (1); Allgemeines zu rationalen Zahlen (2); Allgemeines zu rationalen Zahlen (3); Rationale Zahlen ordnen (1); Rationale Zahlen ordnen (2); Rationale Zahlen im Diagramm (1); Rationale Zahlen im Diagramm (2); Rationale Zahlen im Diagramm (3); Betrag und Gegenzahl (1); Betrag und Gegenzahl (2); Veränderungen (1); Veränderungen (2); Lernzielkontrolle (1); Lernzielkontrolle (2); Gegenzahlenmemory

Arbeitsmittel und Methoden

7-10. Klasse

Sekundarstufe 1

16 Seiten

Arbeitsmittel und Methoden

7-10. Klasse

Sekundarstufe 1

16 Seiten

Verwandte Themen

Einheit

Lösen nach bestimmten Rastern

Alphametik; Magisches Quadrat; Rechenpyramide; Rechenschlange; Rückwärtsrechnen; Zahlenreihen

Geometrie

5-13. Klasse

Sekundarstufe 1

6 Seiten

Geometrie

5-13. Klasse

Sekundarstufe 1

6 Seiten

Entwicklung des Zahlenverständnisses und Modelle der Zahlenverarbeitung

Einheit

Entwicklung des Zahlenverständnisses und Modelle der Zahlenverarbeitung

Erste Schritte auf dem Weg zum Verständnis der Zahlen und der Zahlenstruktur; Klassische Modelle zum frühen Umgang mit Mengen und Zahlen; Neuere Entwicklungsmodelle des Erwerbs früher mathematischer Kompetenzen; Neuropsychologische Modelle der numerischen Kognition

Additive Zerlegung

1-13. Klasse

Grundschule

40 Seiten

Additive Zerlegung

1-13. Klasse

Grundschule

40 Seiten

Einheit

Wiederholung

Bruchschreibweise notieren und zeichnen; Gemischte Schreibweise; Brüche erweitern 1; Brüche erweitern 2; Brüche kürzen 1; Brüche kürzen 2; Brüche ordnen 1; Brüche ordnen 2; Brüche mit gleichen Nennern addieren; Brüche mit ungleichen Nennern addieren; Gemischte Zahlen addieren; Brüche mit gleichen Nennern subtrahieren; Brüche mit ungleichen Nennern subtrahieren; Gemischte Zahlen subtrahieren

Arithmetik

5-9. Klasse

Förderschule

14 Seiten

Arithmetik

5-9. Klasse

Förderschule

14 Seiten