Unterrichtsmaterialien Mathematik: Einheiten
3823 MaterialienIn über 3823 Dokumenten und Arbeitsblättern für das Fach Mathematik findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Mehr Themen
Mathematik
Auswählen
9
Auswählen

Einheit
Grüne Welle - was geht?

Einheit
"Die Differenz 5 kommt ja nur einmal vor!"

Einheit
Woher kommt das Loch?
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten.

Einheit
MathCityMap

Einheit
Zeichen für den Frieden
Verwandte Themen
Einheit
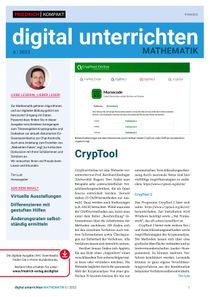
digital unterrichten – Mathematik –6/2022

Einheit
Modellieren im Stochastikunterricht

Einheit
Gesichtserkennung

Einheit
Information

Einheit
Einführung mit Zusatzmaterial

Einheit
Information

Einheit
MINT Zirkel – Ausgabe 3, September 2022

Einheit
MINT Zirkel – Ausgabe 2, Juni 2022

Einheit
Vom Runden zur Genauigkeit

Einheit
Erkunden und Entdecken - ertragreich für Lernende mit unterschiedlichen Lernvoraussetzungen
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀