Unterrichtsmaterialien Mathematik
3250 MaterialienIn über 3250 Dokumenten und Arbeitsblättern für das Fach Mathematik findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Auswählen
Auswählen
Auswählen
Auswählen
3250 Materialien
Einheit
Quadratische Funktionen - Teil 5Nullstellen von quadratischen Funktionen; Abschlusskompetenzcheck
Nullstellen
7-10. Klasse
Gymnasium
8 SeitenNullstellen7-10. KlasseGymnasium8 SeitenTesten kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
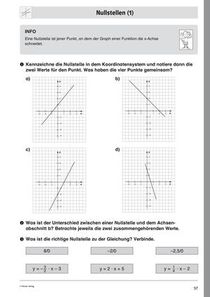
Lineare FunktionenStation 1: Proportionale Funktionen; Station 2: Definitionsbereich und Punktprüfung; Station 3: Proportionalitätskonstante und Steigung I; Station 4: Proportionalitätskonstante und Steigung II; Station 5: Steigungsdreieck; Station 6: y-Achsenabschnitt; Station 7: Nullstellen; Station 8: Vermischte Aufgaben I; Station 9: Vermischte Aufgaben II; Lernzielkontrolle: Lineare Funktionen
Ableitung6-10. KlasseSekundarstufe 122 SeitenAbleitung6-10. KlasseSekundarstufe 122 Seiten
Einheit
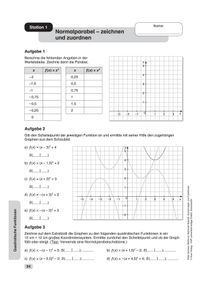
Quadratische FunktionenStation 1: Normalparabel – zeichnen und zuordnen; Station 2: Normalparabel – Punktprobe und zeichnen; Station 3: Stauchen und Strecken; Station 4: Quadratische Ergänzung; Station 5: Die allgemeine Form; Station 6: Nullstellen; Station 7: Rainbow Bridge; Station 8: Eisbärfütterung im Zoo; Station 9: Grundlagen – Wiederholung; Station 10: Vermischte Übungen; Lernzielkontrolle: Quadratische Funktionen
Ableitung6-10. KlasseSekundarstufe 114 SeitenAbleitung6-10. KlasseSekundarstufe 114 Seiten
Einheit
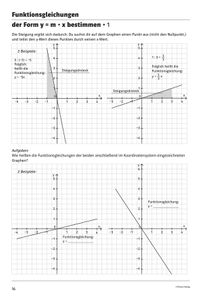
#einfachmathemagisch - Lineare Funktionen – Teil 2Funktionsgleichungen der Form y = m • x bestimmen; Lineare Funktionen der Form y = m • x + n; Erstellung von Wertetabellen und Einzeichnen der Graphen in das Koordinatensystem (y = m • x + n); Funktionsgleichungen der Form y = m • x + n bestimmen; Nullstellen bestimmen; Schnittpunkte bestimmen
Nullstellen7-10. KlasseRealschule13 SeitenNullstellen7-10. KlasseRealschule13 SeitenVerwandte Themen
Einheit
Lineare Funktionen – Teil 4Nullstellen; Lernzielkontrolle
Nullstellen7-10. KlasseSekundarstufe 18 SeitenNullstellen7-10. KlasseSekundarstufe 18 Seiten
Einheit
Quadratische Funktionen – Teil 4Normalform und Scheitelform; Nullstellen; Anwendungsaufgaben; Lernzielkontrolle
Nullstellen7-10. KlasseSekundarstufe 112 SeitenNullstellen7-10. KlasseSekundarstufe 112 Seiten
Einheit
Quadratische FunktionenÜbersicht; Normalform quadratischer Funktionen; Scheitelpunktform quadratischer Funktionen; Nullstellen und Schnittpunkte quadratischer Funktionen; Linearform quadratischer Funktionen; Umkehrung quadratischer Funktionen; Ökonomische Anwendungen quadratischer Funktionen; Zusammenfassung
Ableitung10-13. KlasseSekundarstufe 214 SeitenAbleitung10-13. KlasseSekundarstufe 214 Seiten
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner
Probezeit, entstehen für dich keine Kosten. 🚀
Probezeit, entstehen für dich keine Kosten. 🚀
