Unterrichtsmaterialien Mathematik
5323 MaterialienIn über 5323 Dokumenten und Arbeitsblättern für das Fach Mathematik findest du schnell die passenden Inhalte für deine nächste Stunde. Jetzt kostenlos testen und mehr Materialien nach der Anmeldung entdecken!
Mehr Themen
Mathematik
Auswählen
5
Auswählen
5323 Materialien
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀
Einheit
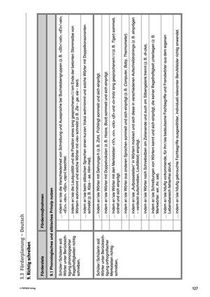
Förderplanung – Vorschläge für Förderziele und FördermaßnahmenFörderplanung – Vorschläge für Förderziele und Fördermaßnahmen
Verwandte Themen
Testen kostet nichts
Probiere meinUnterricht 14 Tage lang aus. Kündigst du während deiner Probezeit, entstehen für dich keine Kosten. 🚀